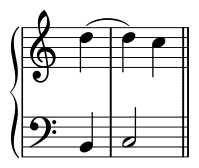Intervall, Intervallum (Zwischenraum, Tonzwischenraum); das Verhältnis zweier Töne von verschiedener Schwingungszahl, oder, anders ausgedrückt, die Vergleichung zweier Tonstufen in Anbetracht ihrer Entfernung voneinander(1). Zwischen dem tiefsten und höchsten in der Musik gebräuchlichen Tone (2C, 16,5 Schwingungen - bis c5, 4224 Schwingungen [pro Sekunde]) liegen soviel Intervalle, als Schwingungszahlen miteinander verglichen werden können. Von einem großen Teil derselben macht die Musik jedoch keinen Gebrauch, indem sie alle Tonverhältnisse ausschließt, welche kleiner sind als der (kleine) halbe Ton. Nur von den in der Praxis als wirkliche Tonstufen vorkommenden Intervallen wird hier die Rede sein. Einige kleine, nur in der Kanonik bei Berechnung der Tonverhältnisse erscheinende Tonabstände werden nur beiläufig berührt, das Notwendige darüber ist in den später anzuführenden Artikeln zu finden.
A. Die Abzählung der Intervalle geschieht auf zweierlei Art. In der Regel geht man vom tieferen Tone aus und rechnet gegen den höheren hin, benennt alsdann das geforderte Intervall mit dem lateinischen Namen derjenigen Zahl von diatonischen Tonstufen, welche man durchschreiten muss, um zu dem gesuchten Tone zu gelangen. Der Ausgangston wird jederzeit als erste Stufe mitgezählt. In manchen Fällen nimmt man jedoch den höheren Ton zum Ausgangspunkt und zählt gegen den tieferen hin, beobachtet aber in Betreff der Bestimmung des Zahlnamens das gleiche Verfahren, so dass hier also der Zahlname die Entfernung des tieferen Tones vom höheren abwärts anzeigt. Nennt man nur den einfachen Zahlnamen (Sekunde, Terz etc.), so ist jederzeit ein aufwärts gerechnetes Intervall darunter zu verstehen. Sollen hingegen Intervalle als abwärts gerechnet begriffen werden, so fügt man ihren Zahlnamen die nähere Bestimmung Unter hinzu, nennt sie Unterintervalle (Untersekund, Unterterz etc.). Diese Unterintervalle sind den in gewöhnlicher Weise aufwärts gerechneten an Zahl und Maß innerhalb der Oktave entgegengesetzt. So ist z. B. c-d aufwärts eine große Sekunde, c-D abwärts aber die kleine Unterseptime; c-f aufwärts eine Quarte, c-F abwärts eine Unterquinte.
Bei Abzählung der Intervalle werden nur die diatonischen Stufen des Liniensystemes - also Linien und Zwischenräume - in Anschlag gebracht. Demnach wird die Entfernung von angenommen e bis c zu sechs Stufen, e-f-g-a-h-c, berechnet, ohne Beachtung der chromatischen Zwischentöne, welche ja keine eigenen Stellen auf dem Liniensystem haben, sondern mit ihren diatonischen Tönen an gleichem Orte liegen. Unser Liniensystem ist ursprünglich nur für diatonische Tonstufen eingerichtet; g-c zum Beispiel macht immer nur vier verschiedene Stufen aus, möge man dieses Intervall vermittelst der diatonischen (g-a-h-c) oder der chromatischen (g-gis-a-ais-h-c) oder auch der enharmonischen Tonleiter (g-gis-as-a-ais-b-h-c) durchmessen. Wollte man das Intervall etwa nach seinem chromatischen Toninhalt abzählen, so würde ein Widerspruch zwischen dem ihm nunmehr beizulegenden Zahlnamen und dem Raum, den es in der diatonischen Skala einnimmt, sich äußern. Jene diatonische Quarte g-c würde, chromatisch gerechnet, eine Sexte ausmachen; damit wäre aber ihrem diatonischen Stufeninhalt widersprochen. Indem also die Intervalle nur nach ihrer diatonischen Stufenzahl gerechnet werden, ändert sich ihr Zahlname auch nicht, wenn das obere oder untere Intervall, oder auch alle beide, eine chromatische Verengerung [sic] oder Erweiterung erfahren. Nachstehende Intervalle unter Beispiel 1a, 1b und 1c sind demnach Sekunden, wenngleich das unter 1a nur einen großen halben Ton, das unter 1b hingegen einen ganzen, und das unter 1c sogar einen ganzen und einen halben Ton enthält. Ebenso sind die Intervalle unter 1d, 1e, 1f Sexten, unter 1g, 1h, 1i Septimen:
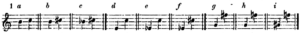
Sekunden, Sexten, Septimen
Das mit seinem Grundton auf derselben Stufe liegende Intervall heißt Prime; über zwei Stufen liegt die Sekunde - und im ferneren werden die dritte, vierte, fünfte, sechste, siebente und achte Tonstufe Terz, Quart, Quint, Sext, Septime und Oktav benannt. Diese lateinischen Zahlnamen schreiben sich aus alter Zeit her. An den Instrumenten ohne Griffbretter gebrauchte man nur den Grundton der Saiten, diese erklangen stets nur ihrer ganzen Länge nach, ohne zur Bildung anderer Töne verkürzt zu werden. Sie wurden mit den Namen prima, secunda, tertia etc. chorda benannt, und diese verblieben auch in späterer Zeit, da man auf ein- und derselben Saite durch Verkürzen verschiedene Tonverhältnisse bilden konnte, den Intervallen.
B. Die vorhin gezeigte mögliche Verschiedenartigkeit des Toninhaltes bei Intervallen von gleicher Stufenzahl und gleichem Zahlnamen erfährt nun eine nähere Bestimmung durch die Beiwörter vollkommen oder rein, groß, klein, übermäßig und vermindert.
1) Mit dem Beinamen vollkommen (perfectum) oder rein werden diejenigen konsonierenden Intervalle(2) bezeichnet, welche nur eine einzige konsonierende Gattung enthalten und sogleich die Eigenschaft der Dissonanz annehmen, sobald eines ihrer Glieder um einen halben Ton erhöht oder erniedrigt wird(3). So beschaffen sind die Prime (Einklang) und Quinte und die im Umfange der Oktave ihnen entgegengesetzten Intervalle Oktave und Quarte. Diese vier Intervalle sind die vollkommenen Konsonanzen. Auch die Quart wird von der Theorie hierzu gerechnet, wenngleich sie in der Praxis häufig, im zweistimmigen Satze sogar jederzeit als Dissonanz behandelt wird(4). Werden die vollkommenen Intervalle ohne Beiwort, also schlechthin Quinte, Quarte etc. genannt, so ist darunter jederzeit die vollkommene Gattung derselben zu verstehen. Über die Annahme der vollkommenen Prime (des Einklanges) als Intervall siehe den Artikel Einklang.
2) Die Bezeichnungen groß und klein gibt man
a) denjenigen Konsonanzen, welche um einen (kleinen) halben Ton verschieden sein können, ohne ihre Eigenschaft als Konsonanzen zu verlieren. Also den Terzen und Sexten. Die Terz c-e ist eine große, denn sie besteht aus zwei ganzen Tönen; die Terz c-es hingegen eine kleine, denn sie enthält nur einen ganzen und einen halben Ton. Beide Gattungen der Terz aber sind, wenn auch unvollkommene Konsonanzen (imperfectae), so doch Konsonanzen überhaupt. Ebenso verhält es sich mit den Sexten, z. B. e-c und e-cis (oder es-c); e-c ist eine kleine Sexte, sie enthält eine reine Quint und einen halben Ton; e-cis oder es-c sind große [Sexten], denn sie enthalten neben der reinen Quint einen ganzen Ton. Große und kleine Sexten sind, gleich den Terzen, unvollkommene Konsonanzen.
b) Unter den Dissonanzen gibt man die Beinamen groß und klein zweien Gattungen der Sekunde und Septime (Dissonantiae per se, quae per se et absolute dissonant). Die kleine Sekunde macht einen (kleinen oder großen) halben Ton aus: h-c, c-des. Die große [Sekunde] ist der ganze Ton: c-d, e-fis. Die Septime ist klein, wenn sie aus einer großen Sexte und einem halben Ton besteht: g-f; groß hingegen, wenn ihr Inhalt eine große Sexte und einen ganzen Ton beträgt: g-fis.
Es ist gleichgültig, mit welchem Gliede des Intervalles die chromatische Veränderung vorgenommen wird, wenn solches aus einem kleinen in ein großes etc. verwandelt werden soll. Es kann ebenso gut am oberen wie am untern Ende geschehen. Aus der kleinen Terz, angenommen c-e♭ [c-es], entsteht eine große ebenso gut durch Erhöhung des oberen Tones, also c-e♮ [c-e], wie durch Erniedrigung des untern, c♭-e♭ [ces-es]. Und ebenso entstehen aus der großen Sext, z. B. e♭-c [es-c], oder aus der großen Septime c-h die kleine Sexte und Septime e♮-c [e-c] und c♯-h [cis-h] durch Erhöhung des untern Tones, wie e♭-c♭ [es-ces] und c-b durch Erniedrigung des oberen.
3) Wird ein reines oder ein großes Intervall um einen (kleinen) halben Ton erweitert (das obere Glied um soviel erhöht, oder das untere Glied um soviel erniedrigt), so entsteht ein übermäßiges (superfluum). Die reine Quinte d-a wird in eine übermäßige verwandelt, indem man a zu ais erhöht oder d zu des erniedrigt. Ebenso ergibt die große Sexte f-d die übermäßige f-dis oder fes-d; die große Sekunde c-d die übermäßige c-dis oder ces-d.
Wird ein reines oder kleines Intervall um einen kleinen halben Ton verengert, indem man das obere Glied um soviel erniedrigt oder das untere um soviel erhöht, so entsteht ein vermindertes (diminutum). Die reine Quint, z. B. d-a, ergibt eine verminderte, indem entweder a zu as erniedrigt oder d zu dis erhöht wird. Auf gleiche Weise entstehen aus der kleinen Septime g-f die verminderten Septimen
gis-f oder g-fes. Dass alle übermäßigen und verminderten Intervalle Dissonanzen sind, ist im Artikel Konsonanz und Dissonanz auseinandergesetzt. Zu erinnern bleibt noch, dass man bei der Intervallbestimmung die enharmonische Mehrdeutigkeit, welche ein und dieselbe Taste auf Klavierinstrumenten hat, wohl auseinanderhalten muss; c-ais ist jederzeit eine übermäßige Sext, c-b hingegen eine kleine Septime, c-as eine kleine Sexte, c-gis aber eine übermäßige Quinte, ces-f eine übermäßige Quart, h-f eine verminderte Quint. Doch kann man hier in der Benennung nicht fehlen, wenn man sich erinnert, dass jederzeit die Stufenzahl den Zahlnamen des Intervalles bestimmt. Gegenwärtig [um 1865] gilt das Verwechseln enharmonischer Töne mit Recht als orthographischer Fehler; im 17. und 18. Jahrhundert nahm man sich hierin noch mehr Freiheiten. So findet man u. a. in Mizler's Übersetzung von Fux, Gradus ad parnassum (S. 57), die Angabe: "Stehet vor g ein ♭, so wird es zu fis, stehet vor a ein ♭, so wird es zu gis. So wird f, e, d zu e, dis, cis, wenn ♭ vorstehen". Man belegte also die durch ein ♭ erniedrigten Töne sprachgebräuchlich mit den Namen der durch ein ♯ erhöhten nächsttieferen. So findet man As-Dur: gis- b-c-cis-dis-f-g-gis und den C-Moll-Akkord c-dis-g benannt. Siehe auch Werckmeister, die nothwendigsten Anmerkungen und Regeln, wie der Basuss cont. oder Generalbass wohl könne tractiret werden, zweite Auflage, 1715. Der Gebrauch bestand noch zu Bachs Zeit.
C. In unserm ganzen, acht Oktaven umfassenden Tonsystem (vom 2C der Orgel bis c5) würden wir, wenn wir alle diatonischen Tonstufen als selbständige Intervalle benennen wollten, deren 56 erhalten (die durch chromatische Veränderung entstehenden ungerechnet). Aber die acht Oktaven dieses ganzen Tonsystems sind an Stufeninhalt einander ganz gleich, wenn auch an Höhe (örtlich) verschieden, alle Töne einer Oktav wiederholen sich in allen übrigen, ein jedes die Oktav überschreitende Intervall liegt also von der Oktav ebenso weit entfernt, wie das innerhalb der Oktav ihm entsprechende vom Grundton: Deshalb rechnen wir die Intervalle nur vom Grundton bis zur Oktave und betrachten alle über letztere hinausgehenden nur als höhere oder tiefere Wiederholungen der vom Grundton aus gerechneten Stufen. Jene heißen einfache, diese zusammengesetzte oder mehrfache Intervalle. C-G ist eine einfache Quinte, C-g eine zusammengesetzte oder doppelte (Doppelquint), C-g1 eine dreifache etc. Die Natur der Intervalle erleidet keine Änderung, wenn ihre oberen oder unteren Glieder um eine oder mehrere Oktaven höher oder tiefer gesetzt werden, C-g oder C-g1 haben ebenso gut die Eigenschaft der reinen Quint, als wenn sie, wie C-G, in der wirklichen Entfernung von fünf Stufen stehen. Deshalb nimmt man die einfachen Intervalle, von der Prime bis zur Oktave, als allen anderen grundleglich an, und nur einige der zusammengesetzten gewinnen in der Harmonie und im Kontrapunkt selbständige Bedeutung als reelle, nicht auf das einfache Verhältnis zum Grundton zu reduzierende Intervalle. Namentlich die neunte Stufe vom Grundton aus, die None; denn das aus zwei Stufen bestehende Intervall, z. B. c-d, wird in der Harmonie auf zwei verschiedene Arten gebraucht, entweder so, dass das untere Glied (Beispiel 2a) oder das obere (2b) die Dissonanz ausmacht.

Nonen
Im ersten Fall, unter 2a, ist das Intervall einfache Sekunde, im zweiten aber reelle None (Nonenvorhalt). Ebenso werden auch die Undezime, im dissonierenden Undezimenakkord (die Quarte der Oktave), sowie die Terzdezime im Terzdezimenakkord (die Sexte der Oktave) als wirkliche Undezime und Terzdezime vom Grundton betrachtet, wenn man diese Akkorde nicht als einfache Dominantharmonie mit dazu angeschlagener Tonika ansehen will, was hier allerdings geschieht. Ferner haben die Dezime und Duodezime in den nach ihnen benannten beiden Arten des doppelten Kontrapunktes reelle Geltung, wenigstens beziehentlich ihres größeren Umfanges, wenngleich die Umkehrung in der einfachen Terz oder Quint der Sache nach völlig mit ihnen übereinkommt.
D. Ältere Theoretiker teilen die vorhin aufgeführten acht Arten einfacher Intervalle in Stamm- und abstammende Intervalle. Jene sind: Grundton, Terz, Quint und Septime; diese die aus jenen durch Umkehrung abgeleiteten Oktavkomplemente: Oktav, Sext, Quart und Sekund. Die Möglichkeit einer Entstehung der Tonleiter aus der Vermischung der abstammenden mit ihren Stammintervallen hier beiseite gesetzt, gibt diese Einteilung doch Gelegenheit zur Erklärung der eben berührten Umkehrung der Intervalle. Man versteht darunter die Vergleichung eines Intervalles mit der Oktave seines Grundtones, statt mit dem Grundton selbst, die Verwandlung desselben in sein Oktavkomplement; oder anders ausgedrückt: Ein Intervall umkehren heißt nichts anderes, als das untere Glied desselben um eine Oktave höher oder das obere um eine Oktave tiefer setzen. Durch dieses Verfahren wird ein Intervall in das im Umfang der Oktave an Zahl und Maß ihm entgegengesetzte umgewandelt. Um das Resultat der Umkehrung zu erfahren, braucht man nur die Zahlen von 1—8 in entgegengesetzter Ordnung untereinander zu schreiben:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Es zeigt sich, dass in der Umkehrung die Prime zur Oktave, die Quinte zur Quarte, die Terz zur Sexte, die Septime zur Sekunde und umgekehrt geworden ist. Die ursprüngliche Intervallzahl hat sich also in die im Umfange von 8 Stufen ihr entgegengesetzte verwandelt. Ebenso verkehrt sich die Gattung der Intervalle, ob klein, groß, übermäßig oder vermindert, mit Ausnahme der reinen, in die entgegengesetzte Größe. Es ist in Bezug darauf also zu merken:
1) Vollkommene (reine) Intervalle geben in der Umkehrung wiederum vollkommene (reine) . Also die vollkommene Prime, Quinte, Quarte und Oktave werden zur vollkommenen Oktave, Quarte, Quinte und Prime.
2) Große Intervalle ergeben in der Umkehrung kleine, kleine demnach große. Große Sekunden, Terzen, Sexten und Septimen haben kleine Septimen, Sexten, Terzen und Sekunden; kleine Sekunden, Terzen, Sexten und Septimen haben große Septimen, Sexten, Terzen und Sekunden zu Oktavausfüllungen; es werden in der Umkehrung z. B. die große Terz c-e zur kleinen Sexte e-c1, die große Septime c-h zur kleinen Sekunde h-c1, die kleine Septime c-b zur großen Sekund b-c1 etc.
3) Übermäßige Intervalle geben verminderte und verminderte geben übermäßige. Die übermäßige Quinte, z. B. c-gis, ergibt die verminderte Quarte gis-c1, die verminderte Quinte h-f die übermäßige Quarte f-h1.
Eine Übersicht aller in der praktischen Musik gebräuchlichen Intervalle, auch ihren Oktavkomplementen entgegengesetzt, bietet die weiter unten stehende Tabelle. Nächst diesen gibt es jedoch, wie vorhin bemerkt, noch eine Anzahl kleinerer Tonabstände, welche weder melodisch noch harmonisch verwendet, höchstens, wenn man will, beim melodischen Herüberschleifen oder Durchziehen eines Melodietones zum nächstfolgenden höheren oder tieferen mitberührt werden. Sie kommen in ungleichschwebenden Temperaturen wie auch in der reinen diatonischen Tonleiter durch Vergleichung der ungleich großen gebräuchlichen Intervalle zum Vorschein. Man hat, um hier nur ein Beispiel zu geben, gefunden, dass wenn man das Verhältnis der großen Terz der reinen diatonischen Tonleiter in zwei Teile teilt, die beiden als ihre Hälften sich ergebenden ganzen Töne nicht von gleicher Größe sein können. Es kommt durch die Teilung ein großer und ein kleiner ganzer Ton zum Vorschein, jener dem Verhältnis 9/8, dieser dem 10/9 entsprechend. Vergleicht man diese beiden Intervalle, um ihre Differenz zu erhalten (subtrahiert 10/9 von 9/8), so findet man dass der Unterschied 81/80 beträgt. Dieses Intervall, um welches der große ganze Ton größer ist als der kleine, nennt man das syntonische oder große Komma (siehe Komma). Besonders merkwürdig [bemerkenswert] ist es, weil es bei Einrichtung eines Tonsystems nach einer schwebenden Temperatur die höchste Abweichung von den ursprünglich reinen Verhältnissen ist, welche die Töne überhaupt vertragen, um allenfalls melodisch brauchbare Verbindungen eingehen zu können.
In unserem heutigen gleichschwebend temperierten Tonsystem sind alle gleichartigen Intervalle einander gleich, jeder Halbton ist (die Oktave zu 1000 angenommen) um 83⅓:1000 vom nächsthöheren und tieferen entfernt. Die durch ein ♯ erhöhten Halbtöne fallen mit den auf der nächsthöheren Stufe liegenden durch ein ♭ erniedrigten auf ein- und derselben Klaviertaste zusammen, und es sollen keine anderen Intervalle, als die auf den Klavierinstrumenten befindlichen, von der Praxis angewendet werden. Dass Sänger und Spieler auf Instrumenten mit bestimmbarer Tonhöhe nichtsdestoweniger die enharmonischen Intervalle unwillkürlich unterscheiden, indem sie unbewusst der natürlich reinen Quintbestimmung folgen, wird bekannt sein. Doch verbieten manche Tonlehrer dieses sogenannte Kommatisieren, als die Reinheit des Zusammenklanges beeinträchtigend, wenn Instrumente mit gleichschwebend temperierter Skala mitwirken.
Jene kleinen, im theoretischen Vortrag gebräuchlichen Intervalle, als neben dem syntonischen Komma das große und kleine Limma, die Diesis, das Schisma und Diaschisma, findet man, soweit hier überhaupt nötig erscheint, in eigenen Artikeln erklärt. Im gleichen ist über Tonverhältnisse überhaupt unter Verhältnis, Teilung der Verhältnisse, Vergleichung der Verhältnisse, Temperatur, Addition und Subtraktion der Intervalle nachzulesen.
E. Tabelle der in der praktischen Musik gebräuchlichen Intervalle(5)
1. Die Prime ist vollkommen (rein) und übermäßig:
a) Die vollkommene Prime, der Einklang, Unisonus, besteht aus zwei Tönen von gleicher Größe oder Schwingungszahl: c-c, c1-c1. Sie muss jederzeit in dem Verhältnis 1:1, das ist, völlig rein, ausgeübt werden.
b) Die übermäßige Prime ist der kleine halbe Ton, dessen beide Glieder im Liniensystem auf ein- und derselben Linie oder in ein- und demselben Zwischenraum liegen: c-cis, es-e. Ihr Verhältnis in der reinen diatonischen Skala ist 25/24 (L. 59); in der gleichschwebenden Temperatur, mit der kleinen Sekunde zusammenfallend, 83⅓:1000 Stufenweite (die Oktave zu 1000 angenommen).
Verminderte Primen gibt es nicht.
2. Die Sekunde ist klein, groß und übermäßig:
a) Die kleine Sekunde ist der auf zwei Stufen liegende große halbe Ton: c-des, h-c, fis-g. Ihr reines Verhältnis ist 16/15 (93), der gleichschwebenden Temperatur 83⅓.
b) Die große Sekunde enthält einen großen und einen kleinen halben Ton in zwei Stufen, oder einen ganzen Ton. Es ist schon erinnert worden, dass es in der reinen diatonischen Skala zweierlei ganze Töne gibt:
1) den großen, im Verhältnis 9/8 (L. 170); von dieser Beschaffenheit sind die Intervalle c-d, f-g und a-h;
2) den kleinen, im Verhältnis 10/9 (152); so beschaffen sind d-e und g-a. Die Differenz zwischen beiden ergab das syntonische Komma 81/80 (18). In der gleichschwebenden Temperatur sind alle ganzen Töne einander gleich (166⅔); die Abweichung der temperierten großen Sekunde von der ursprünglichen reinen beträgt -3½.
c) Die übermäßige Sekunde enthält einen ganzen und einen kleinen halben Ton: c-dis, d-eis, as-h. Reines Verhältnis ist 75/64 (L. 229).
Von der verminderten Sekunde gilt ein Gleiches wie von der verminderten Prime.
3. Die Terz ist vermindert, klein und groß:
a) Die verminderte Terz enthält zwei große halbe Töne (16/15) in drei Stufen: cis-es, dis-f. Reines Verhältnis 256/225 (186).
Wenn auch auf gleichschwebend temperierten Klavierinstrumenten die verminderte Terz mit der großen Sekunde auf gleichen Tasten zusammenfällt, so sind doch beide, wie alle enharmonisch zusammenfallenden Intervalle, in der Orthographie voneinander zu unterscheiden: cis-es ist eine verminderte Terz; cis-dis oder des-es sind aber große Sekunden, weil sie nur zwei Stufen auf dem Liniensystem einnehmen.
Selbstverständlich dissoniert die verminderte Terz wie alle anderen verminderten Intervalle. Einzelne Theoretiker jedoch, welche das Verhältnis 7 der natürlichen Tonreihe (die zu kleine Septime der Hörner und Trompeten) als konsonierend annahmen, sprachen auch von einer konsonierenden verminderten Terz 7:6 (auf dem Horn g-b). Wir machen von dieser zu kleinen Septime keinen Gebrauch (die Hörner müssen den Ton etwas treiben, um die kleine Septime b harmonisch brauchbar zu geben), folglich auch nicht von der angeblich konsonierenden verminderten Terz, dessen oberes Glied sie ist.
b) Die kleine Terz enthält einen ganzen und einen großen halben Ton in drei Stufen: c-es, cis-e, e-g. Ihr reines Verhältnis ist 6/5 (263), ihr temperiertes 3.83⅓ = 250, demnach beträgt die Abweichung der temperierten kleinen Terz von der reinen -13, oder etwa ⅔ des syntonischen Kommas.
c) Die große Terz besteht aus einem großen und einem kleinen ganzen Ton in drei Stufen: c-e, fis-ais, es- g. Reines Verhältnis 5/4 (322); temperiertes 333⅓, also um +11⅓ vom reinen abweichend.
Übermäßige Terzen (125/96, L. 381) kommen in harmonischen Verhältnissen nicht vor.
4. Die Quart ist vermindert, rein und übermäßig:
a) Die verminderte Quarte besteht aus einem ganzen und zwei großen halben Tönen in vier Stufen, oder aus einer kleinen Terz und einem großen halben Ton: cis-f, e-as. Ihr reines Verhältnis ist 32/25 (356).
b) Die reine Quarte enthält zwei ganze Töne und einen großen halben Ton in vier Stufen: c-f, fis-h. Reines Verhältnis 4/3 (415), temperiertes 416⅔, um +1⅔ vom reinen abweichend.
c) Die übermäßige Quart, drei ganze Töne (zwei große mit einem kleinen in der Mitte) in vier Stufen enthaltend, daher auch Tritonus genannt: f-h, c-fis. Reines Verhältnis 45/32 (492), temperiertes 500, als Hälfte der Oktave, mit der verminderten Quinte auf einer Klaviertaste zusammenfallend.
5. Die Quinte ist vermindert, rein und übermäßig:
a) Die verminderte Quint enthält zwei ganze und zwei große halbe Töne in fünf Stufen: h-f, cis-g. Reines Verhältnis 64/45 (508), temperiertes 500, mit der übermäßigen Quarte zusammenfallend.
b) Die reine Quint besteht aus drei ganzen und einem großen halben Ton in fünf Stufen: c-g, e-h, es-b. Reines Verhältnis 3/2 (585); zwölf reine Quinten (=7020) übersteigen aber sieben Oktaven (=7000), welche sie ausmachen, um das Komma 20. Indem nun die Oktave stets nur in völliger Reinheit ausgeübt werden darf und keine Abweichung verträgt, wird jede der 12 Quinten im temperierten System um 1/12 des Komma 20 tiefer gestimmt (zu 583⅓), also von der ursprünglich reinen Quint um -1⅔ abweichend, woraus sich dann die richtige Zahl von 7000 für zwölf Quinten oder sieben Oktaven ergibt. Jene Abweichung ist aber so gering, dass sie der Wahrnehmung des Gehöres durchaus entgeht.
c) Die übermäßige Quint ist zusammengesetzt aus vier ganzen Tönen in fünf Stufen, oder aus zwei großen Terzen: c-gis, b-fis. Ihr reines Verhältnis ist demnach gleich deren Summe 25/16 (644), ihr temperiertes 666⅔, mit der kleinen Sexte zusammenfallend.
6. Die Sexte ist klein, groß und übermäßig:
a) Die kleine Sexte enthält drei ganze und zwei große halbe Töne in sechs Stufen: e-c, fis-d. Reines Verhältniss 8/5 (678), temperiertes 666⅔, um -11⅓ von jenem abweichend.
b) Die große Sexte besteht aus vier ganzen Tönen und einem großen halben Ton in sechs Stufen: c-a, e-cis. Reines Verhältniss 5/3 (737), temperiertes 750, also um +13 jenes übersteigend.
c) Die übermäßige Sext macht fünf ganze Töne in sechs Stufen aus: f-dis, c-ais. Reines Verhältnis 225/128 (778), temperiertes 833⅓.
7. Die Septime ist vermindert, klein und groß:
a) Die verminderte Septime ist aus drei ganzen und drei großen halben Tönen in sieben Stufen zusammengesetzt: gis-f, cis-b. Reines Verhältnis 128/75 (771), ihr temperiertes fällt mit der großen Sexte auf eine Taste des Klavieres.
b) Die kleine Septime beträgt vier ganze und zwei große halbe Töne auf sieben Stufen: g-f, c-b. Reines Verhältnis 16/9 (830), auch 9/5, (848), temperiertes 833⅓, woraus sich ergibt, dass die temperierte kleine Septime um 3⅓ höher ist als die natürliche.
c) Die große Septime, fünf ganze Töne und einen großen halben Ton in sieben Stufen enthaltend: c-h, cis-his, hat im reinen Verhältnis 15/8 (907), im temperierten 916⅔.
8. Die Oktave ist rein und vermindert:
a) Die reine Oktave besteht aus fünf ganzen und zwei großen halben Tönen in acht Stufen. In allen Arten gleich- oder ungleich schwebender Temperaturen wird sie unabänderlich in ihrem ursprünglich reinen Verhältnis 2 ausgeübt.
b) Die verminderte Oktav endlich hat vier ganze und drei große halbe Töne in acht Stufen: cis-c1, dis-d1. Reines Verhältnis 48/25 (941), temperiertes 916⅔, mit der großen Septime auf einer Klaviertaste.
Übermäßige Oktaven und Septimen, desgleichen verminderte Sexten kommen in harmonischen Verhältnissen nicht vor.
Nachstehende Übersicht gibt diese Intervalle noch einmal kurz ihren Oktavausfüllungen gegenübergestellt:

alle Intervalle - Übersicht
Eine Übersicht der Intervalle mit ihrem Inhalt an großen und kleinen, ganzen und halben Tönen steht noch unter Ganzer Ton. Näheres über die Intervallenlehre ist zu finden in: Glarean, Dodecachordon, Basel 1547, Lib. I., S. 18-28. Riedt, "Versuch über die musikalischen Intervalle…", Berlin 1753. Riedt, "Beantwortung der in des Herrn Capellmeister Scheibe historisch critischen Vorrede zu seiner Abhandlung von dem Ursprung und Alter der Musik § 9 befindlichen Anmerkung über F. W. Riedt's Versuch über die musikalischen Intervallen"; Marpurg's historisch-kritische Beitrage Bd. I. 5. Stück, Nr. 2. Riedt, "Zwo musikalische Fragen […], Marpurg's historisch-kritische Beiträge Bd. III. 5. Stück, Nr. 1. Joh. Ad. Scheibe, Abhandlung von den musikalischen Intervallen und Geschlechtern, Hamburg 1739. G. Phil. Telemann's neues musikalisches System, nebst Schröter's Beurtheilung desselben, in der Mizler'schen Bibliothek, Bd. III. Th. 4, S. 713; auch in Scheibe's Abhandlung von der musikalischen Composition, Leipzig 1773. J. L. Röllig, Versuch einer musikalischen Intervallentabelle…, Leipzig 1789. J. Andr. Sorge, Geschlechtsregister der Intervalle nach Anleitung der Klänge, so das grosse Waldhorn giebt, Hof 1741. Sulzer, Theorie der schönen Künste, Leipzig 1792, Abhandlung und Tabelle, Bd. II. S. 694. Walthers Lexikon, verschiedene Worterklärungen.
1 Intervallum est vocis a voce, seu soni acuti gravisque distantia. Luc. Lossius. Erotemata mus. pract. 1590.
2 Siehe Konsonanz und Dissonanz.
3 Das Wort rein, in dieser mit vollkommen gleichgeltenden Bedeutung, ist hier nicht auf Stimmungsreinheit zu beziehen und soll nicht die Unreinheit zum Gegensatze haben. Doch wäre es auch in letzterem Sinne noch nicht unrichtig; zwar sind im gleichschwebenden System alle Intervalle mit Ausnahme der Prime und Oktav nicht völlig rein, doch weichen die vollkommenen Konsonanzen weniger von der natürlich reinen Tonbestimmung ab als die übrigen Kon- und Dissonanzen, daher sie diesen gegenüber verhältnismäßig noch immer als rein oder wenigstens als der Reinheit am nächsten kommend gelten können. Siehe Rein.
4 Siehe Konsonanz und Dissonanz [sowie] Quart.
5 In älteren Lehrbüchern findet man öfter die Verhältnisse der Intervalle auch nach der Kirnbergerschen ungleichschwebenden Temperatur angegeben. Diese aber hat, wenngleich [in] ihrer Zeit hochangesehen, heute alle Geltung verloren (siehe Temperatur), weshalb ihre Zahlenangaben hier fortbleiben. Es sind nur die Verhältnisse aufgeführt, welche nach der von Zarlino aufgestellten, sogenannten reinen diatonischen Skala den Intervallen zukommen, außerdem die einfachen Proportionalzahlen der Logarithmen (die Oktav = 1000 angenommen) nach der jetzt [um 1865] gebräuchlichen gleichschwebenden Temperatur.
[Dommer Musikalisches Lexicon 1865, 458ff]