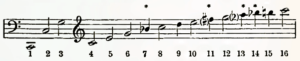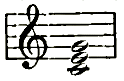Musiklexikon: Was bedeutet Klang?

Rubrik: Klang / Musik-Lexikon 1882 | Autor:

Klang (1882)

Klang nennt man die hörbaren Schwingungen elastischer Körper, d. h. Klang ist die wissenschaftliche Bezeichnung dessen, was der Laie Ton nennt. Man sagt [um 1880] völlig gleichbedeutend: das Instrument hat einen schönen, weichen "Klang" oder "Ton".

Die Akustik unterscheidet Klang und Geräusch und versteht unter letzterem den durch unregelmäßige, unter erstem den durch regelmäßige Schwingungen hervorgebrachten Gehörseindruck. Regelmäßige Schwingungen sind solche, welche sich mit gleicher Geschwindigkeit der Folge wiederholen, wie die des Pendels einer Uhr. Da von der Geschwindigkeit der Folge (Periode) der Einzelschwingungen die Höhe des gehörten Tons abhängt, so geben Schwingungen von sich gleichbleibender Periode Töne oder Klänge von konstanter Tonhöhe.

Seit man weiß, dass die Klänge unserer Musikinstrumente nicht einfache Töne, sondern aus einer Reihe einfacher Töne zusammengesetzt sind, welche bei angespannter Aufmerksamkeit wohl unterscheidbar sind, aber gewöhnlich nicht unterschieden werden, hat das Wort Klang in der Wissenschaft die allgemeinere Bedeutung erhalten, während man unter "Ton" den einfachen Ton als Teil des Klangs versteht. Der Klang wird seiner Höhe nach bestimmt nach der Tonhöhe der tiefsten und (in der Regel) stärksten der ihn zusammensetzenden Töne, die man auch Teiltöne, Partialtöne, Aliquottöne nennt. Da alle übrigen Teiltöne höher liegen als der dem Klang den Namen gebenden Grundton, Fundamentalton, Hauptton, so nennt man sie gewöhnlich Obertöne, versteht aber unter dem zweiten Oberton nicht den dritten Ton der Reihe, sondern den zweiten. Insofern die übrigen Töne für gewöhnlich über dem Grundton überhört werden, heißen sie auch Beitöne, sofern sie in einem nahen verwandtschaftlichen (harmonischen) Verhältnis zu jenem stehen, auch harmonische Töne (sons harmoniques [französisch], nicht: Harmonikatöne). Die Reihe der ersten 16 Partialtöne ist z. B. für den Ton C:

Klang (Riemann 1882)

Obertonreihe

Die in halben Noten gegebenen Töne sind sämtlich Bestandteile des Durakkords des Grundtons (C-Dur-Akkord), und es unterliegt keinem Zweifel, dass die Konsonanz des Durakkords (Durkonsonanz) auf die Obertonreihe bezogen werden muss, d. h. dass ein Durakkord, gleichviel in welcher Umlagerung der Töne, aufzufassen ist als ein Klang, in dem diese oder jene Obertöne verstärkt sind (die den selbständig hervorgebrachten Tönen des Akkords entsprechenden). Folgende Beispiele mögen das verdeutlichen; der dem Akkord nachgesetzte tiefe Ton ist der Grundton des Klanges, als dessen Vertreter der Akkord anzusehen ist:

Klang (Riemann 1882)

C-Dur-Akkorde

Der hier angezeigte Grundton des vertretenen Klanges ist sogar jederzeit als Kombinationston vorhanden. Es ergänzt sich aber die Reihe der Partialtöne nicht allein durch die Kombinationstöne bis hinab zum Klanggrundton, sondern sie setzt sich auch nach der Höhe hin fort durch die Obertonreihen der Akkordtöne. Aus diesem Grund ist es ganz natürlich, dass heute für das musikalische Hören auch noch weit höhere Obertöne als die im einzelnen Klang (Ton eines Instruments) noch unterscheidbaren eine große Rolle spielen. Denn in der [um 1880] modernen harmonischen Musik werden durch den Akkord schon sehr hoch liegende Obertöne in ungewöhnlicher Stärke hervorgebracht, und noch höhere kommen als deren nächste Obertöne hinzu; die einstimmige Musik des Altertums und frühen Mittelalters dagegen musste sich notwendigerweise innerhalb eng gezogener Grenzen harmonischer Verständlichkeit bewegen, weil für sie nur die nächsten Obertöne in Betracht kommen konnten.

Die oben [im ersten Notenbeispiel] mit * bezeichneten Partialtöne stimmen nicht genau in der Tonhöhe mit den sie repräsentierenden Noten überein. Eine selbständige Hervorbringung derselben im Akkord wird nämlich nicht mehr im Sinn der Obertonreihe verstanden, vielmehr werden dieselben dann immer im Sinn von annähernd entsprechenden, im Mollsinn verwandten Tönen (siehe weiter unten) aufgefasst. Das geschieht überhaupt mit allen den Obertönen von dem siebten an, deren Ordnungszahlen Primzahlen sind. Diejenigen aber, deren Ordnungszahlen Produktzahlen sind (9=3x3, 15=3x5, 25=5x5 etc.), werden als Obertöne der Obertöne, als sekundäre Obertöne, verstanden, d. h. als integrierende Bestandteile der primären (der 9. als 3. des 3., der 15. als 5. des 3. etc.). Werden dieselben im Akkord vertreten, d. h. in gleicher Stärke mit primären hervorgebracht, so wirken sie als Dissonanz. Es erscheint dann der primäre Oberton, dessen Obertöne sie sind, selbst als Klanggrundton, so dass zwei Klänge auf einmal vertreten sind. Eine Ausnahme macht nur das einfachste Verhältnis, das von 2:1, das Oktavverhältnis, dessen Potenzierung niemals eine Dissonanz ergibt. Auch können alle anderen Intervalle um eine oder mehrere Oktaven erweitert oder verengert werden, ohne ihre Harmoniebedeutung zu verändern. Streichen wir deshalb alle Oktavtöne aus der Obertonreihe weg, so bleiben als verschiedenartige Bestandteile der Durkonsonanz des Oberklangs nur übrig der Grundton (1), die Duodezime (3) und Septdezime (5). Die Urgestalt des Durakkords ist deshalb nicht eigentlich der Dreiklang in enger Lage,

Klang (Riemann 1882)

C-Dur, enge Lage

sondern die weite Lage:

Klang (Riemann 1882)

C-Dur, weite Lage

Die Ordnungszahlen der Partialtöne repräsentieren zugleich die relativen Schwingungszahlen der durch sie gebildeten Intervalle, z. B. ist das Schwingungsverhältnis des 15. zum 16. Oberton (Leittonverhältnis h:c) = 15:16. Vergleiche Intervall. Dass der Wohlklang gewisser in neuerer Zeit (Wagner) sehr beliebter Dissonanzen wohl auf die annähernde Übereinstimmung mit höheren Obertönen bezogen werden muss (z. B. c, e, b, fis' = 4:5:7:11), sei nicht vergessen.

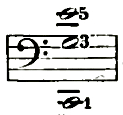
Die Konsonanz des Mollakkords ist aus der Obertonreihe nicht zu erklären, und alle Versuche, dies dennoch zu tun (Helmholtz), müssen zu Resultaten führen, die den Musiker nicht befriedigen. Dagegen hat eine vollkommen gegensätzliche Betrachtungsweise den gewünschten Erfolg. Längst vor Entdeckung der Obertöne bezog man die Durkonsonanz auf die Saitenteilung 1-1/6, d. h. 1 ist die Saitenlänge des Grundtons, 1/2 die der Oktave, 1/3 die der Duodezime usw. bis zum 6. Partialton. Die Mollkonsonanz dagegen bezog man auf die Umkehrung der Reihe, also auf die Saitenlängen 1-6, d. h. 1 ist der Hauptton, 2 die Unteroktave, 3 die Unterduodezime etc. Diese Auffassung der Mollkonsonanz als polarischen Gegensatzes der Durkonsonanz findet sich, soviel mir [Hugo Riemann] bekannt, zuerst bei Zarlino im 30. Kapitel der "Istitutioni armoniche" (1558), wird auch von Tartini (1754 u. 1767), der, wie Zarlino, einer der gelehrtesten und geistreichsten Theoretiker gewesen ist, und in neuester Zeit seit M. Hauptmann (1853) durch eine große Anzahl junger Theoretiker mit mehr oder minder Konsequenz (O. Kraushaar, O. Tiersch, O. Hostinsky) sowie mit voller Schärfe und Konsequenz von A. v. Öttingen und dem Herausgeber dieses Lexikons [Hugo Riemann] verfochten. Die Mollkonsonanz ist in ganz derselben Weise auf eine Untertonreihe zu beziehen wie die Durkonsonanz auf die Obertonreihe. Die akustischen Phänomene, welche die Annahme dieser Untertonreihe rechtfertigen, sind das des Mittönens und das der Kombinationstöne. Ein klingender Ton bringt klangfähige Körper zum Mittönen, deren Eigenton einem seiner Untertöne entspricht, oder, was dasselbe ist, von deren Eigenton er Oberton ist. Allerdings machen die mittönenden Körper zunächst starke partielle Schwingungen (mit so viel Knoten, dass der erregende Ton hervorgebracht wird), aber sie machen daneben auch (schwächere und daher schwerer wahrnehmbare) totale. Der tiefste Kombinationston eines Intervalls ist immer der erste gemeinsame Unterton beider Intervalltöne, z. B. für e':g'=C, für c'':d'' ebenfalls C, aber auch für e':d''=C usw. Die Reihe der 16 ersten Untertöne ist, wenn wir c''' als Ausgangston (Hauptton) nehmen:

Klang (Riemann 1882)

Untertonreihe nach Riemann

Die Ordnungszahlen der Untertöne repräsentieren die relativen Saitenlängen derselben. Die Schwingungsverhältnisse würden ausgedrückt werden durch die Reihe der einfachen Brüche: 1, 1/2, 1/3 etc., ebenso wie umgekehrt die relativen Saitenlängenverhältnisse für die Töne der Obertonreihe durch die Reihe der einfachen Brüche dargestellt würden; zum Beispiel ist die Oktave c:c' im Sinn der Obertonreihe (c=1 angenommen) hinsichtlich der relativen Schwingungszahlen durch 1:2, hinsichtlich der Saitenlängen aber als 1:1/2, im Sinn der Untertonreihe dagegen (c' als 1 angenommen) hinsichtlich der Schwingungszahlen als 1:1/2, hinsichtlich der Saitenlängen aber als 1:2 zu bezeichnen. Der 1., 2., 3., 4., 5., 6., 8., 10., 12., 16. etc. Überhaupt alle Töne der Untertonreihe, welche tieferen Oktaven des 1., 3. und 5. Untertons entsprechen, sind ganz ebenso Bestandteile des Mollakkords unter c, des c-Unterklangs, wie dieselben Zahlen der Obertonreihe den Durakkord über dem Hauptton, dem Oberklang (im oben gegebenen Beispiel den C-Dur-Akkord), ergeben. Der 7., 11., 13. Unterton, überhaupt alle Primzahlen entsprechenden vom 7. an, sind für Akkordbildungen so wenig brauchbar wie die primären Obertöne vom 7. an. Die Produktzahlen entsprechenden aber (9=3x3, 15=3x5 etc.) sind als sekundäre Untertöne ebenso dissonant gegen den Hauptton des Unterklangs wie die sekundären Obertöne gegen den Hauptton des Oberklangs. Sie werden, wie jene, nicht direkt auf den Hauptton bezogen, sondern durch Vermittlung primärer Partialtöne, von denen sie wiederum primäre Partialtöne sind, d. h. sie vertreten deren Klänge, so dass ihre Hervorbringung mit primären Untertönen im Akkord als gleichzeitige Vertretung zweier Klänge Dissonanz ist. Vergleiche Klangfolge und Dissonanz. [Riemann Musik-Lexikon 1882, 454ff]

Rubrik: Handwörterbuch Musik 1807 / Klang | Autor:

Klang (1807)

Klang. Alles was unser Ohr empfindet, ist Wirkung eines von einem Körper erregten und auf eine gewisse Art sich [sic] schwingenden Luftstromes, der unsere Gehörnerven trifft und ihnen die Art seiner Schwingungen mitteilt. Sind diese Schwingungen der Luftteile so beschaffen, dass unser Gefühl nichts gleichartiges in der Fortdauer derselben wahrnimmt, wie z. B. bei dem Fahren eines Wagens, so nennen wir die Wirkung, die sie auf unser Ohr machen, Geräusch. Ist der Körper, durch welchen die Luftteile in Schwingungen oder Oszillationen gesetzt werden, nicht elastisch, so kann er nicht erzittern oder einige Zeit lang Schwingungen machen und also der Luft auch keine Fortsetzung gleichartiger Schwingungen mitteilen. Von dieser Beschaffenheit ist z. B. der Schlag auf ein Stück Blei. Die Wirkung, die solche nicht gleichartig fortgesetzten Schwingungen der Luftteile auf unser Ohr machen, nennt man Schall. Werden aber die Luftteile durch einen elastischen Körper in Schwingungen gesetzt, so hat ein solcher Körper vermöge seiner Elastizität die Eigenschaft, dass er nach einem erlittenen Druck oder Schlage eine Zeit lang gleichartig erzittert - oder Schwingungen macht, die in gleichen Zeiträumen aufeinander folgen. Dieses lässt sich an einer aufgespannten und mit dem Finger gerissenen [gezupften] Saite sehr deutlich wahrnehmen. Durch diese gleichartigen Schwingungen des Körpers werden die Luftteile ebenfalls zu einer Fortsetzung gleichartiger Schwingungen veranlasst. Weil aber die einzelnen Schwingungen der Luftteile so geschwind aufeinander folgen, dass wir keinen Zwischenraum der Zeit dabei wahrnehmen, so entsteht in uns das Gefühl eines einige Zeit lang gleichartig fortgesetzten Schalls, welches wir Klang nennen.

Betrachtet man zwei klingende Saiten von gleicher Stärke und Spannung, deren eine aber merklich kürzer ist als die andere, so sieht man, dass die Schwingungen der kürzeren in kleineren Zeiträumen aufeinander folgen als die Schwingungen der längeren. Diese Verschiedenheit der gleichartigen Schwingungen, in Ansehung der Geschwindigkeit ihrer Folge, erregt bei dem Gefühle des Klanges eine sehr bestimmte Modifikation desselben, so, dass wir den langsameren Grad der Schwingungen von dem geschwinderen sehr deutlich unterscheiden können. Wir sind gewohnt, das Gefühl des langsameren Grades der Schwingungen mit dem Wort tief, das Gefühl eines damit verglichenen geschwinderen Grades derselben aber mit dem Worte hoch zu bezeichnen.

Werden nun höhere und tiefere Klänge in ein bestimmtes Verhältnis ihrer Höhe und Tiefe gebracht, so nennt man sie Töne.

Weil die Höhe und Tiefe des Tones von dem Grade der Geschwindigkeit und dieser Grad der Geschwindigkeit der Schwingungen von der Länge der Saite (oder überhaupt von der Größe des sonoren Körpers) abhängt, so müssen notwendig Größe des sonoren Körpers, Geschwindigkeit der Schwingungen, die er veranlasst, und Höhe oder Tiefe des Tons, welcher dadurch erzeugt wird, in Proportion stehen. Diese Wahrheit ist das Prinzip derjenigen Wissenschaft, die man Kanonik nennt.

Der Klang hat überdies noch folgende Eigenschaften:

  1. breitet er sich von dem Orte, wo er entsteht, nach allen Richtungen aus;
  2. dringt er durch feste Körper;
  3. hat er die Eigenschaft, dass er von entfernten Körpern in gerader Richtung zurückgeworfen werden kann, siehe Echo;
  4. kann er für sich betrachtet, rein, unrein, rau, sanft, stark, schwach usw. sein. Die Unreinheit des Klanges entsteht aus der Beimischung ungleichartiger Schwingungen. Wenn z. B. bei einer Darmsaite die verschiedenen Fäden, aus welchen sie besteht, nicht egal zusammengedreht sind, so dass der eine lockerer als der andere angespannt ist, so entstehen Nebenschwingungen, die notwendig eine Beimischung eines Nebenklanges mit dem Hauptklange verursachen müssen.
    Das sanfte oder rauhe des Klanges hängt teils von der Materie, teils von der Form des Körpers ab, von welchem er hervorgebracht wird. Die Stärke oder Schwäche desselben ist Wirkung der größeren oder geringeren Menge der in Schwingung gesetzten Luftteile.
  5. hat der Klang die Eigenschaft, dass er zugleich mehrere von ihm verschiedene Töne mit sich hören lässt. Mann nennt diese Eigenschaft desselben, von der man sich am besten durch das Spiel der Aeolsharfe überzeugen kann, die Sympathie der Töne.
  6. Diejenigen, die sich bemüht haben, die Ursachen dieses Mitklingens mehrerer Töne in einem einzigen Klang zu entdecken, haben gefunden, dass eine aufgespannte Saite sich nicht allein ihrer ganzen Länge nach schwingt und das Gefühl ihres Klanges erregt, sondern dass auch zugleich die Hälfte, der dritte, vierte und die folgenden Teile einer solchen Saite, jeder für sich, noch besondere Schwingungen macht, wodurch das Mitklingen anderer Töne bewirkt wird. Diejenigen Punkte, bei welchen sich die schwingende Saite in solche kleinere Teile teilt, werden Schwingungsknoten genannt.
  7. ist der Klang so beschaffen, dass die Schwingungen, die ihn erregen, im Stande sind, leichte Körper in gewisse Richtungen zu werfen, welche den Verhältnissen der Töne angemessen sind. Wenn man z. B. einen ungefähr 8 Zoll langen und 1 Zoll breiten Striemen von einer Glastafel an gewissen bestimmten Oertern [sic] mit der Spitze des Daumens und des Mittelfingers der linken Hand festhält, und die Kante dieses Glasstriemens mit einem Violinbogen anstreicht, so kann man demselben z. B. nicht allein die Quinte, Quarte und Terz seines Haupttones entlocken, sondern die verschiedenen Schwingungen, welche das Glas bei diesen verschiedenen Tönen macht, werfen zugleich einen auf dasselbe ganz dünne gestreuten feinen Streusand in Linien, die den Verhältnissen dieser Töne entsprechen; denn sobald einer dieser Töne erklingt, springen alle Sandkörner auf dem Glasstriemen nicht allein in eine Longitudinallinie, sondern es formieren sich auch zugleich ebenso viel Transversallinien, als nötig sind, um dieses oder jenes Intervall hervorzubringen. Hieraus hat man die Folge gezogen, dass es sowohl Longitudinal- als Transversalschwingungen geben müsse.
    Zu diesen Eigenschaften des Klanges gehört endlich noch,
  8. dass zwei Klänge von einem bestimmten Verhältnisse, das heißt, dass zwei Töne durch ihr Erklingen einen tieferen dritten Klang (sono terzo) in der Luft erzeugen können. Wenn man z. B. die Töne g und c' auf der Violine, und zwar in einem Zimmer oder Saale, in welchem der Wiederschall nicht durch Tapeten oder andere Wandverzierungen gehemmt wird, völlig rein intoniert, so erzeugt sich der Ton des großen C von selbst in der Luft. Es gehören aber mehrmals wiederholte Versuche dazu, ehe man einen Ort findet, wo dieses Experiment zu unserer völligen Befriedigung glückt.

[Koch Handwörterbuch Musik 1807, 199ff]