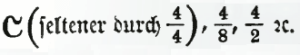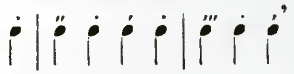Metrik (1882)
Metrik ist in der Musik die Lehre von den Taktarten, den Unterteilungen der Taktglieder und den Zusammenfassungen mehrerer Takte zu Bildungen größerer Ausdehnung. Die Metrik hat es mit der Aufstellung der leeren Schemata zu tun, während die Rhythmik das musikalische Leben innerhalb dieser Schemata betrachtet. Hält man an dieser Unterscheidung fest, so wird eine klare Abhandlung beider Disziplinen nicht schwer sein. Wir haben dann unter metrischen Akzenten die durch das metrische Schema gegebenen zu verstehen, unter rhythmischen dagegen solche, welche durch die Stellung rhythmischer Motive innerhalb der Schemata bedingt werden.
Die einfachste metrische Bildung ist der Takt, welcher sein kann:
- zweiteilig, vorgezeichnet als
2/1, 2/2, 2/4, 2/8 [etc.];
- dreiteilig, vorgezeichnet als 3/1, 3/2, 3/4, 3/8 etc.
Andere nicht unterteilbare Taktarten kommen selten oder gar nicht vor. Die wenigen vorkommenden fünf- oder gar siebenteiligen Takte sind und bleiben Kuriositäten.
Nun kann aber der zwei- und dreiteilige Takt in verschiedener Gestalt auftreten, je nach der metrischen Akzentuation. Der zweiteilige Takt kann sein:
zweiteiliger Takt
Der dreiteilige kann sein:
- volltaktig
- einfach auftaktig
- doppelt auftaktig
dreiteiliger Takt
Unser Taktstrich markiert nicht den Beginn des metrischen Fußes, sondern nur die Stelle des metrischen Akzents, der daher immer der Note nach dem Taktstrich zufällt. die nicht mit dem Akzent beginnenden Füße sind sämtlich auftaktig, ragen aus einem Takt in den anderen (französisch: à cheval).
Eine Anzahl neuer metrischer Bildungen erhalten wir, wenn wir entweder die einzelnen Taktglieder der einfachen Taktarten gleichmäßig in kleinere Werte auflösen (unterteilen) oder mehrere Takte zusammenfassen. Das Resultat ist in beiden Fällen dasselbe. Die Zusammenfassung zweier zweiteiliger Takte resp. die Zweiteilung jedes Taktglieds eines zweiteiligen ergibt den vierteiligen Takt, vorgezeichnet durch C (seltener 4/4), 4/8, 4/2 etc.
Vierertakt
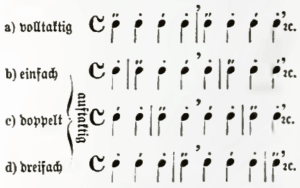
Derselbe kann (hinsichtlich der Akzentuation) in vier verschiedenen Gestalten auftreten:
- volltaktig
- einfach auftaktig
- doppelt auftaktig
- dreifach auftaktig
vierteiliger Takt
Je zwei Taktglieder stehen hier je zwei anderen gegenüber und weisen gegeneinander dasselbe Verhältnis auf wie die beiden Taktglieder des einzelnen zweiteiligen Taktes; bei a) und b) [1) und 2)] folgt der stärker betonten ('') die leichter betonte (') Hälfte, bei c) und d) [3) und 4)] umgekehrt der leichter betonten die stärker betonte. Diese letztere Art der Betonung hat gegenüber der ersteren etwas Aufgeregteres, Treibendes, sie ist die diastaltische Akzentuation der alten Griechen im Gegensatz zur hesychastischen (ruhigen) von a) und b).
Die nächste metrische Bildung ist der sechsteilige Takt (6/2, 6/4, 6/8, 6/16), d. h. die Vereinigung zweier dreiteiliger Takte resp. die Unterdreiteilung des zweiteiligen Taktes (zwei Triolen). Die möglichen Akzentuationen sind:
- volltaktig
- einfach auftaktig
- doppelt auftaktig
- dreifach auftaktig
- vierfach auftaktig
- fünffach auftaktig
d. h. a)-c) [1)-3)] hesychastisch, d)-f) [4)-6)] diastaltisch.
sechsteiliger Takt
Die Unterzweiteilung des dreiteiligen Taktes resp. Vereinigung dreier zweiteiliger Takte pflegt nicht besonders vorgezeichnet zu werden, sondern wird durch 3/2, 3/4 etc. ausgedrückt. Die sich ergebenden Bildungen sind aber immerhin der Betrachtung wert:
- volltaktig
- einfach auftaktig
- doppelt auftaktig
- dreifach auftaktig
- vierfach auftaktig
- fünffach auftaktig
dreiteiliger Takt
Der neunteilige Takt (9/8, 9/4, 9/16) ist die Zusammenfassung dreier dreiteiliger oder die Unterdreiteilung eines dreiteiligen (3/3); seine möglichen Akzentuationen sind:
- volltaktig
- einfach auftaktig
- zweifach auftaktig
- dreifach auftaktig
- vierfach auftaktig
- fünffach auftaktig
- sechsfach auftaktig
- siebenfach auftaktig
- achtfach auftaktig
neunteiliger Takt
Die übrigen möglichen Bildungen sind nach demselben Prinzip leicht übersichtlich zusammenzustellen: Der achtteilige Takt, als Unterzweiteilung des vierteiligen, der selbst schon eine Unterteilung des zweiteiligen ist, hat dreierlei Akzente:
achtteiliger Takt
Der zwölfteilige Takt (12/4, 12/8, 12/16) desgleiche als Unterteilung des vier-, drei- oder sechsteiligen, nämlich:
zwölfteiliger Takt
Der achtzehnteilige als Unterteilung des sechs-, drei- oder neunteiligen:
achtzehnteiliger Takt
Endlich sind die größten der üblichen Arten zusammengesetzter Takte, der 16-teilige und 24-teilige, mit vier Stufen der Akzentuation zu denken, zum Beispiel:
24-teiliger Takt
Eine noch weiter Verfolgung der Möglichkeiten hat wenig Sinn. Mehr als dreifache Abstufungen der metrischen Akzentuation werden kaum durchführbar sein, zumal im konkreten Fall die rhythmischen und pathetischen Akzente noch variierend hinzukommen (vergleiche Rhythmik).
Die theoretische Betrachtung der metrischen Schemata führt zu der Erkenntnis, dass uns ein Zeichen fehlt, welches die höhere Einheit mehrerer Takte, das Kolon der alten Griechen, markiert, ein Taktstrich höherer Ordnung, welcher den Sitz des metrischen Hauptakzents andeutet, d. h. besagt, ob die Akzentuation der Takte die hesychastische oder diastaltische sein soll. Das einzige Auskunftsmittel, das bisher dem Komponisten zum bestimmten Ausdruck seiner Intention zu Gebote steht, ist die Anwendung zusammengesetzter Taktarten, die indes für viele Fälle allzu unförmlich ausfallen würden (z. B. im 12/4- oder 18/4-Takt). Man könnte vielleicht zu der alten Form der Taktstriche (um 1600) zurückgreifen, welche nicht durch das ganze Liniensystem, sondern nur durch die obere Hälfte desselben gehen, und diese kleinen Taktstriche zur Markierung der gewöhnlichen Takte, die jetzt üblichen großen dagegen zur Markierung der Hauptakzente reservieren. Der Anfang der ersten Sonate von Beethoven (Op. 2, I) hat das Metrum
Beethoven, Op. 2, I
d. h. achtteilig fünffach auftaktig, und wäre daher zu notieren:
Beethoven, achtteilig fünffach auftaktig
Die von Beethoven für as'' und b'' vorgeschriebenen Akzente (>) wären dann übrig. Es ist die Aufgabe der Zukunft, diese von R. [Rudolf] Westphal angeregten Ideen zu verarbeiten und dadurch die Notenschrift zu vervollkommnen. [Riemann Musik-Lexikon 1882, 580ff]
