Großer ganzer Ton. Die fünf ganzen Töne, welche in der diatonischen Tonleiter zwischen den Grenzen einer Oktave enthalten sind, können nicht in gleicher Größe oder in einem gleichen Verhältnisse ausgeübt werden. Von der Notwendigkeit der Verschiedenheit derselben wird man teils durch die natürliche Entstehungsart der Töne vermittelst der Teilung einer Saite, von der in dem Artikel Verhältnis gehandelt wird, teils aber auch durch die Teilung der Intervalle und durch die Addition und Subtraktion ihrer Verhältnisse überzeugt. Wenn man zum Beispiel die große Terz c-e harmonisch teilt, als:(1)
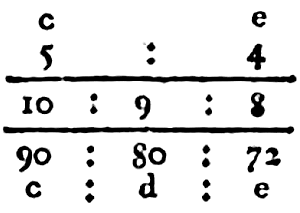
so kommen die beiden ganzen Töne [Ganztonschritte] c-d und d-e, in welche sie durch diese Teilung zerfällt, in verschiedener Größe zum Vorscheine, nämlich der Ton c-d in dem Verhältnisse 9:8 und d-e in dem Verhältnisse 10:9.(2) Weil nun das Verhältnis des Tones c-d, nämlich 9:8, um das syntonische Komma (81:80) größer ist als das Verhältnis des Tones d-e oder 10:9,(3) so nennt man jenen den großen, diesen hingegen den kleinen ganzen Ton.(4) […]
1 Das dabei zum Grunde liegende Verfahren wird in dem Artikel Teilung der Verhältnisse zergliedert.
2 Auf welche Art die oben bei der harmonischen Teilung der Terz zum Vorschein kommenden Verhältnisse 90:80 und 80:72 abgekürzt oder auf ihre Wurzelzahlen 9:8 und 10:9 reduziert werden, findet man in dem Artikel Reduktion der Verhältnisse.
3 Siehe Vergleichung der Verhältnisse.
4 Diese Verschiedenheit des ganzen Tones, und zwar in den angezeigten Verhältnissen 9:8 und 10:9, wurde schon in dem ersten Jahrhunderte der christlichen Zeitrechnung von Didymus gefunden. Vorher bedienten sich die Griechen des ganzen Tones jederzeit in einerlei Tongröße, nämlich in dem Verhältnis 9:8. Weil nun dadurch die große Terz, die aus zwei ganzen Tönen besteht, bis zum Übelklange zu hoch und dadurch das Verhältnis derselben zu weit von der Unität entfernt wurde, weil es die Verbindung zweier großer ganzer Töne 81:64 ausmachte, so war dieses ohne Zweifel eine der Hauptursachen, warum die Terzen von den Griechen unter die Dissonanzen gerechnet wurden.
[Koch Musikalisches Lexikon 1802, 686f]


